트리는 연결된 노드로 이루어진 계층적인 구조를 표현하는 가장 널리 사용되는 추상적인 자료 구조다. 각각의 노드는 많은 자식과 연결될 수 있지만 항상 하나의 부모만 가져야 한다.

그래프의 일종으로 한 노드에서 시작해서 자기 자신에게 돌아오는 순환이 없는 연결 그래프이다. 트리는 비선형적 계층 구조로 이루어져 있다. 마치 나무를 뒤집어 놓은 듯한 모양을 하고 있어 트리라고 부른다. 쉽게 컴퓨터의 폴더 구조를 생각하면 된다.

용어

• 루트 노드 (root node): 부모가 없는 노드로 최상단의 노드.
• 단말 노드 (leaf node): 자식이 없는 노드로 터미널 (terminal) 노드라고도 불림.
• 내부 노드 (internal node): 단말 노드가 아닌 노드.
• 형제 (sibling): 같은 부모를 갖는 노드.
• 링크 (link): 노드와 노드사이를 잇는 선이다. edge, branch라고도 불림.
• 깊이 (depth): 루트 노드에서 한 노드에 도달하기까지의 링크 수.
• 차수 (degree): 한 노드가 가지는 링크 수.
• 너비 (width): 한 레벨에 있는 노드의 개수.

특징

• N개의 노드를 갖는 트리는 항상 N-1개의 링크를 가진다.
• 한 노드에서 어떠한 노드로 가는 길은 한 개의 유일한 경로를 가진다.

이진 트리 (Binary Tree)

자식 노드를 최대 2개까지만 가질 수 있는 트리이다.

이진 트리 종류

• 완전 이진 트리(Complete binary tree): 왼쪽 자식 부터 채워지며, 단말 노드를 제외한 모든 노드가 채워져 있다.
• 균형 이진 트리(Balanced binary tree): 노드의 왼쪽과 오른쪽의 하위 트리와의 높이가 1이상 차이가 나지 않는 이진 트리다.

트리 순회

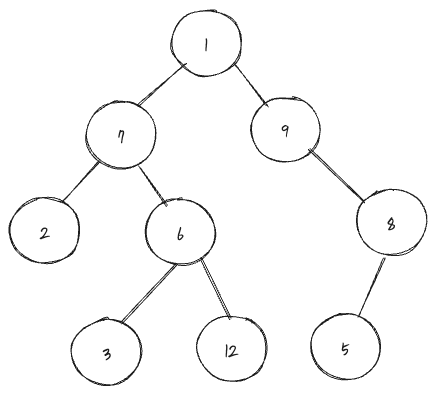
• 중위 순회 (In-Order traversal): 왼쪽 -> 루트 -> 오른쪽 순서로 순회하는 방식을 말한다.
  • 결과: 2, 7, 3, 6, 12, 1, 9, 5, 8
• 후위 순회 (Pre-Order traversal): 루트 -> 왼쪽 -> 오른쪽 순서로 순회하는 방식을 말한다.
  • 결과: 1, 7, 2, 6, 3, 12, 9, 8, 5
• 전위 순회 (Post-order traversal): 왼쪽 -> 오른쪽 -> 루트 순서로 순회하는 방식을 말한다.
  • 결과: 2, 3, 12, 6, 7, 5, 8, 9, 1

이진 탐색 트리 (Binary Search Tree, BST)

• 이진 트리의 조건을 만족하면서 아래의 정렬 조건을 만족하는 트리이다.
  • 모든 노드의 값은 유일하다.
  • 부모의 값이 왼쪽 자식의 노드보다 크다.
  • 부모의 값이 오른쪽 자식의 노드보다 작다.

만약 BST가 포함된 문제가 나오면 보통 O(n)의 시간보다 빠르기를 기대한다.

시간 복잡도

일반적인 유형

많은 트리 문제에서는 일반적으로 다음과 같은 문제들에 대한 해결책을 요구한다.

• 값 삽입
• 값 삭제
• 트리의 노드 개수 구하기
• 값이 트리에 있는지 구하기
• 트리의 높이 구하기
• 이진 탐색 트리
  • 이진 탐색 트리인지 확인
  • 최대값 구하기
  • 최소값 구하기

기법

재귀 사용

재귀는 트리를 탐색을 위한 가장 일반적인 접근법이다. 만약 서브트리가 문제 전체를 풀 수 있다고 생각되면, 재귀를 사용해라.
재귀를 사용할 때는 항상 노드가 null인 경우에 대해서 생각해야 한다.

레벨 탐색

레벨 탐색을 사용하도록 요구되면 BFS를 사용할 수 있다.

필수 문제

• Binary Tree
  • LeetCode
    • Maximum Depth of Binary Tree
    • Invert/Flip Binary Tree
• Binary Search Tree
  • LeetCode
    • Lowest Common Ancestor of a Binary Search Tree

추천 연습 문제

• Binary tree
  • LeetCode
    • Same Tree
    • Binary Tree Maximum Path Sum
    • Binary Tree Level Order Traversal
    • Lowest Common Ancestor of a Binary Tree
    • Binary Tree Right Side View
    • Subtree of Another Tree
    • Construct Binary Tree from Preorder and Inorder Traversal
    • Serialize and Deserialize Binary Tree
• Binary search tree
  • LeetCode
    • Validate Binary Search Tree
    • Kth Smallest Element in a BST

참조
Array cheatsheet for coding interviews | Tech Interview Handbook