그래프 (Graph)

그래프는 객체(정점, 혹은 노드)와 객체 사이를 연결하는 간선으로만 이루어진 자료구조이다. 트리또한 순환을 갖지 않는 그래프의 일종이다.
그래프는 보통 정렬되지 않는 관계들을 모델링 위해 사용된다. (사람 사이의 관계, 장소간의 거리 등)
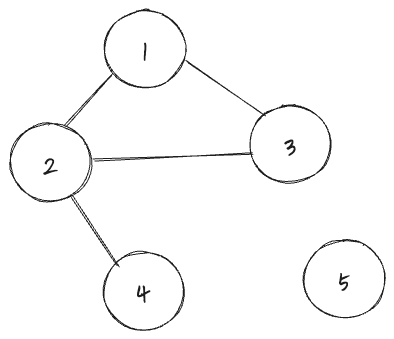
코딩테스트에서 그래프는 보통 이차원 행렬로 Input이 주어진다. 따라서 이차원 행렬을 탐색하는데 익숙해지는 것이 중요하다.
트리와 그래프의 차이점
트리와 그래프의 차이점을 표로 정리하면 다음과 같다.
| 그래프 | 트리 | |
|---|---|---|
| 방향성 | 방향 그래프, 무방향 그래프 | 방향 그래프 |
| 순환 | 순환 가능, 자체 순환도 가능 | 순환 불가능 |
| 루트 노드 | 루트 노드 개념 없음 | 루트 노드는 한 개만 존재 |
| 부모-자식 | 부모-자식 개념 없음 | 부모-자식 관계를 가지며 모든 자식은 하나의 부모만 가짐 |
| 모델 | 네트워크 모델 | 계층 모델 |
| 순회 | DFS, BFS | |
| 간선의 수 | 정해지지 않음 | N개의 노드는 항상 N-1개의 간선을 가짐 |
| 경로 | 다양 | 임의의 두 노드간의 경로는 유일 |
| 예시 및 종류 | 지도, 지하철 노선도의 최단 경로, 선수 과목 | 이진 트리, 이진 탐색 트리 |
- 그래프에 존재하는 모든 간선을 한 번만 통과하면서 처음의 노드로 되돌아오는 경로
- 간선의 개수가 짝수일 때만 존재
용어
- 정점(vertex): 데이터가 저장되는 위치라는 개념이다. 노드(node)라고도 부른다.
- 간선(edge): 정점과 정점 사이를 연결하는 선이다.
- 인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점
- 차수(degree): 한 정점에 연결된 간선의 수
- 진입 차수(in-degree): 방향 그래프일 때 외부에서 들어오는 간선의 수
- 진출 차수(out-degree): 방향 그래프일 때 외부로 나가는 간선의 수
- 경로(path): 한 정점에서 정점으로 가는 길의 정점을 나열한 것 (e.g. 1→2→3→5)
- 경로 길이(path length): 경로를 구성하는 간선의 수
- 단순 경로(simple path): 경로의 정점들이 모두 다른 정점인 경로
그래프의 종류
무방향 그래프
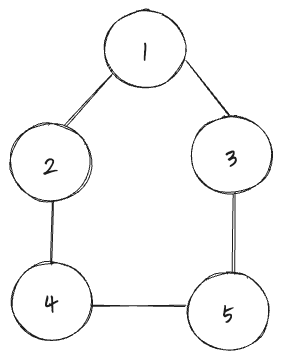
- 정점사이의 간선에 방향이 없는 그래프를 말한다.
- 간선을 통해서 양방향으로 갈 수 있다.
- (A, B)로 표현한다. (A, B) = (B, A)
방향 그래프
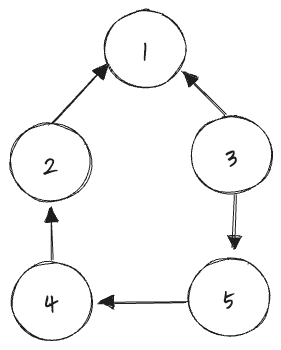
- 정점사이의 간선에 방향이 있는 그래프를 말한다.
- 한 방향만으로 이동할 수 있다.
- A -> B는 <A, B>로 표현한다. <A, B> != <B,A>
가중치 그래프
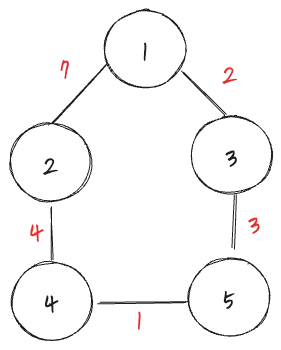
- 간선에 비용이 추가되는 그래프를 말한다.
- 네트워크라고도 한다. (지도상의 거리, 통신망의 요금 등)
완전 그래프
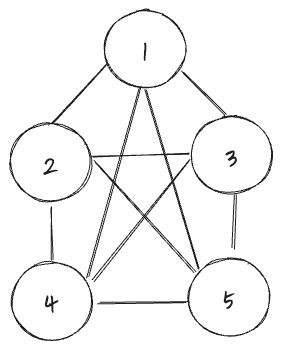
- 모든 정점이 서로 연결된 그래프를 말한다. 최대의 간선수를 가진다.
- 정점이 N개인 무방향 그래프의 간선 수: N*(N-1)/2 개
- 정점이 N개인 방향 그래프의 간선 수: N*(N-1)개
연결 그래프

- 서로 다른 모든 정점들 사이에 간선이 있는 그래프를 말한다.
비연결 그래프
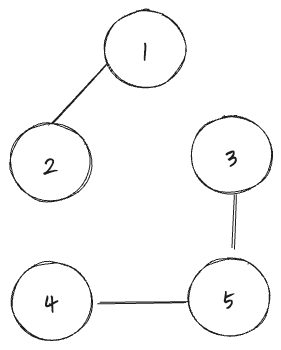
- 연결이 되지 않는 정점이 있는 그래프를 말한다.
그래프 구현
그래프를 구현하는 방법에는 인접행렬을 이용하여 구현하는 방법과 인접리스트를 이용해 구현하는 방법이 있다.
인접행렬
그래프의 정점들을 2차원 배열로 만들고, 각 노드들이 인접 정점일 경우 1을 아니라면 0으로 채워준다.
무방향 그래프
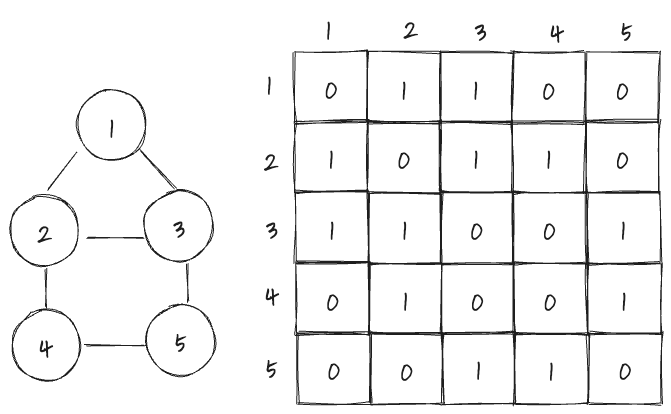
방향 그래프
방향 그래프의 경우 행->열로 가는 정점에 간선이 있다면 1, 아니면 0을 채워준다.
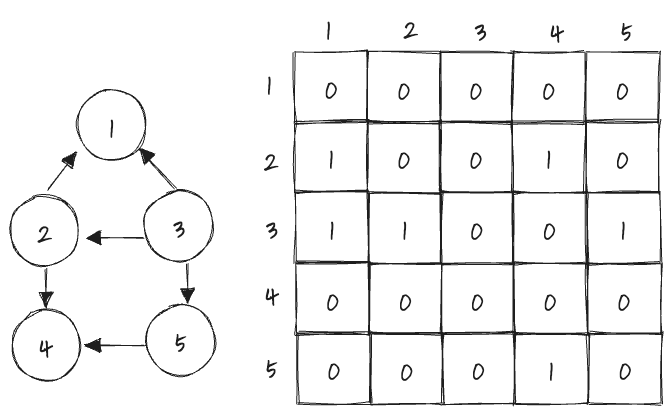
인접행렬로 구현시 장점
- 두 점에 대한 연결 정보를 조회할 때 시간 복잡도는 O(1) 이다.
- 구현이 비교적 간단하다.
인접행렬로 구현시 단점
- 모든 정점에 대해 정보를 대입해야 하므로 O(n^2)의 시간 복잡도가 소요된다.
- 필요 이상의 공간이 낭비 된다.
인접 리스트
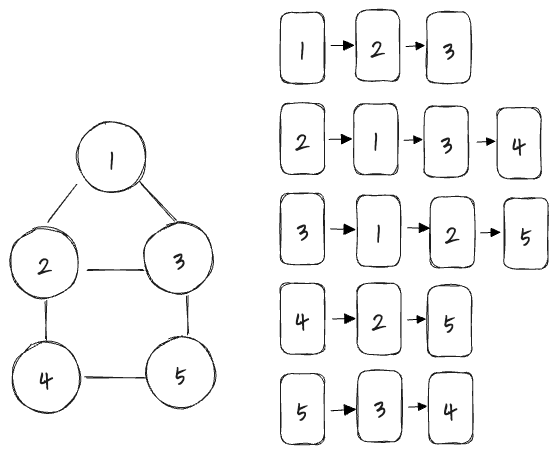
무방향 그래프
각 정점을 헤드로잡고 인접 정점들을 전부 연결 리스트로 연결한다.
방향 그래프
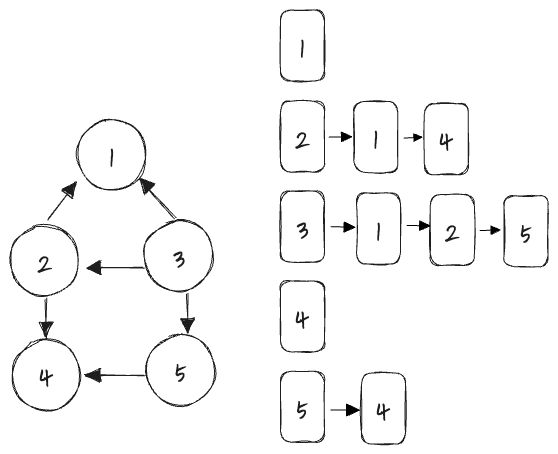
방향 그래프의 경우 각 정점에서 시작해 진출 차수가 있는 노드들을 연결해 준다.
인접리스트로 구현시 장점
- 정점에 연결된 정점 정보를 탐색할 때 시간 복잡도는 O(n)이다.
- 필요한 만큼의 공간만 사용한다.
인접리스트로 구현시 단점
- 특정 두 점의 연결 정보를 알려고 할 때 인접행렬보다 시간이 오래 소요된다.
- 구현이 비교적 어렵다.
인접리스트 VS 인접행렬
희소 그래프
정점이 간선보다 더 많은 경우를 희소 그래프라고 한다.
예를 들어 정점이 1000개인데 간선은 10개인 그래프가 있다고 하자. 그렇다면 10개의 간선을 표현하기 위해 1000x1000 행렬을 만들어야 한다. 하지만 이를 연결 리스트로 구현하면 1010(정점 수 + 간선 수)개의 노드만으로 구현할 수 있다.
밀집 그래프
간선이 정점보다 더 많은 경우를 밀집 그래프라고 한다.
이번에는 반대로 100개의 정점이 있고, 1000개의 간선이 있다고 해보자. 이 경우에는 리스트보다 행렬로 구현하는 것이 더 좋다. 왜냐하면 행렬의 경우 두 정점을 연결하는 간선을 조회할 때 O(1)의 시간 복잡도만 소요되기 때문이다.
| 인접행렬 | 인접리스트 | |
|---|---|---|
| 공간 복잡도 | O(V^2) | O(V+E) |
| 시간 복잡도 | O(1) | O(n) |
| 구현 그래프 | 밀집 그래프 | 희소 그래프 |
그래프 탐색 알고리즘
- 일반적인 경우: BFS (Breadth First Search), DFS (Depth First Search)
- 일반적이지 않은 경우: Topological Sort, 다익스트라 알고리즘(Dijkstra's algorithm
필수 문제
- LeetCode
- Number of Islands
추천 연습 문제
- LeetCode
- Breadth-first search
- Either search
- Topological sorting
참조
Array cheatsheet for coding interviews | Tech Interview Handbook